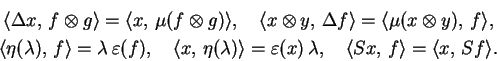


Next: Příklad 3: algebra funkcí
Up: Hopfovy algebry
Previous: Příklad 1: algebra funkcí
Obsah
Buď opět 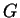 konečná grupa a nechť
konečná grupa a nechť
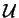 je grupová algebra
je grupová algebra 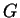 .
.
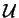 je vektorový prostor, jehož bázi tvoří elementy grupy
je vektorový prostor, jehož bázi tvoří elementy grupy 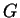 ,
tedy prvky
,
tedy prvky
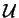 jsou lineární kombinace
jsou lineární kombinace
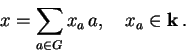 |
(40) |
Opět
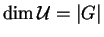 . Násobení stačí předepsat na bazických vektorech
. Násobení stačí předepsat na bazických vektorech 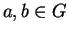 a v tom případě se shoduje s grupovým násobením v
a v tom případě se shoduje s grupovým násobením v 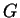 ,
,
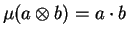 .
Dále
.
Dále
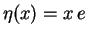 ,
, 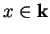 .
Obdobně konásobení, kojednotku a antipode stačí
předepsat na prvcích báze. Definujeme
.
Obdobně konásobení, kojednotku a antipode stačí
předepsat na prvcích báze. Definujeme
Příklady 1 a 2 jsou navzájem duální.
Párováním mezi
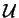 a
a 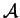 nazveme bilineární zobrazení (
nazveme bilineární zobrazení (
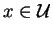 je tvaru (40))
je tvaru (40))
Vlastnosti, které párování musí splňovat,
jsou tyto: je nedegenerované
(
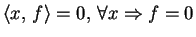 a obdobně pro druhý argument) a splňuje rovnosti
a obdobně pro druhý argument) a splňuje rovnosti
Zde využíváme toho, že párování mezi
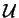 a
a 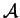 indukuje párování
mezi
indukuje párování
mezi
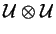 a
a
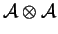 :
:



Next: Příklad 3: algebra funkcí
Up: Hopfovy algebry
Previous: Příklad 1: algebra funkcí
Obsah
Pavel Stovicek
2000-02-25
![]() konečná grupa a nechť
konečná grupa a nechť
![]() je grupová algebra
je grupová algebra ![]() .
.
![]() je vektorový prostor, jehož bázi tvoří elementy grupy
je vektorový prostor, jehož bázi tvoří elementy grupy ![]() ,
tedy prvky
,
tedy prvky
![]() jsou lineární kombinace
jsou lineární kombinace
![]() a
a ![]() nazveme bilineární zobrazení (
nazveme bilineární zobrazení (
![]() je tvaru (40))
je tvaru (40))