Metoda orbit je vlastně geometrická konstrukce reprezentací Lieových algeber
a grup. Postup je shodný s geometrickým kvantováním, ovšem symplektické variety
a třídy funkcí, které chceme kvantovat (přiřadit jim operátory), jsou přesně
vymezeny a přirozeně závisí na dané Lieově grupě. I v případě metody orbit se
nebudeme pouštět do podrobného výkladu a omezíme se na ilustrativní příklad,
kterým bude Lieova grupa ![]() .
.
Nejprve přece jen několik obecných poznámek. Nechť
![]() je Lieova algebra
a
je Lieova algebra
a
![]() duální vektorový prostor. Hodnotu funkcionálu
duální vektorový prostor. Hodnotu funkcionálu
![]() na vektoru
na vektoru
![]() budeme značit jako
budeme značit jako
![]() (tím je zdůrazněna dualita mezi prostory
(tím je zdůrazněna dualita mezi prostory
![]() a
a
![]() ). Každému
prvku
). Každému
prvku
![]() přiřadíme lineární funkci
přiřadíme lineární funkci ![]() na
na
![]() vztahem
vztahem
Na
![]() existuje právě jedna Poissonova závorka, která splňuje
existuje právě jedna Poissonova závorka, která splňuje
Zmiňme se o vztahu mezi symplektickými a poissonovskými varietami. V předcházející
části jsme využili přechodu od symplektické formy k Poissonově závorce. V opačném
směru platí následující obecný výsledek. Na každé poissonovské varietě
![]() existuje jednoznačně určené rozvrstvení (tzv. foliace), jehož všechny listy
jsou symplektické podvariety variety
existuje jednoznačně určené rozvrstvení (tzv. foliace), jehož všechny listy
jsou symplektické podvariety variety ![]() . V obecném případě mohou být ve
foliaci zastoupeny listy různé, ale vždy nutně sudé dimenze. Je-li
. V obecném případě mohou být ve
foliaci zastoupeny listy různé, ale vždy nutně sudé dimenze. Je-li
![]() list foliace, potom Poissonova závorka na
list foliace, potom Poissonova závorka na
![]() určená příslušnou symplektickou
strukturou je rovna zúžení původní Poissonovy závorky definované na
určená příslušnou symplektickou
strukturou je rovna zúžení původní Poissonovy závorky definované na ![]() :
:
Rovněž na duálním prostoru
![]() existuje jednoznačně určená foliace,
jejíž listy jsou symplektické variety. Tyto listy se přesně shodují s orbitami
tzv. koadjungované (coadjoint) akce. Blíže se touto akcí zabývat nebudeme, ale
názvosloví ``orbita'' se přidržíme. V metodě orbit se vychází právě z těchto
orbit coby symplektických variet a kvantují se funkce na dané orbitě
existuje jednoznačně určená foliace,
jejíž listy jsou symplektické variety. Tyto listy se přesně shodují s orbitami
tzv. koadjungované (coadjoint) akce. Blíže se touto akcí zabývat nebudeme, ale
názvosloví ``orbita'' se přidržíme. V metodě orbit se vychází právě z těchto
orbit coby symplektických variet a kvantují se funkce na dané orbitě
![]() získané zúžením funkcí
získané zúžením funkcí ![]() (7).
(7).
Lieova algebra
![]() je tvořena antihermitovskými maticemi rozměru
je tvořena antihermitovskými maticemi rozměru
![]() s nulovou stopou. Zvolme bázi (tradiční, až na komplexní jednotky
Pauliho matice)
s nulovou stopou. Zvolme bázi (tradiční, až na komplexní jednotky
Pauliho matice)
Dále na
![]() zavedeme symetrickou bilineární formu vztahem
zavedeme symetrickou bilineární formu vztahem
Pro jednoduchost pišme ![]() místo
místo
![]() . Podle
definice (7) a ztotožnění (11) máme
. Podle
definice (7) a ztotožnění (11) máme
Podle (8) je Poissonova závorka na
![]() jednoznačně určena rovnostmi
jednoznačně určena rovnostmi
Poissonova závorka na libovolné poissonovské varietě splňuje Leibnizovo pravidlo:
V případě Lieovy závorky (8) definované na duálu
![]() k Lieově algebře
k Lieově algebře
![]() pišme
pišme ![]() místo
místo
![]() .
Zobrazení
.
Zobrazení
V případě závorky (12) budeme opět pro jednoduchost psát ![]() místo
místo
![]() . Snadný výpočet dává
. Snadný výpočet dává
Buď
![]() sféra o poloměru
sféra o poloměru ![]() . Na
. Na
![]() zvolíme lokální
komplexní souřadnice
zvolíme lokální
komplexní souřadnice
![]() :
:
Pro určení Poissonovy závorky na
![]() stačí vypočítat
stačí vypočítat
![]() .
Přitom uplatníme pravidlo
.
Přitom uplatníme pravidlo
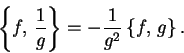
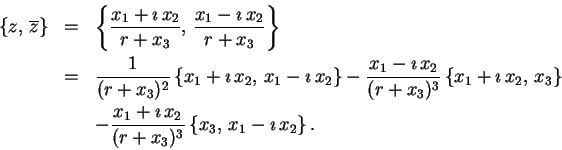
Vektorová pole příslušná souřadnicovým funkcím:
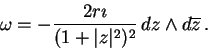
Zvolme další systém komplexních souřadnic
![]() tak, abychom
pokryli celou sféru, a sice
tak, abychom
pokryli celou sféru, a sice
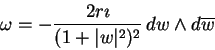
Zvolme nyní pro souřadné systémy ![]() a
a ![]() po řadě 1-formy
po řadě 1-formy ![]() a
a ![]() s vlastností
s vlastností
![]() :
:
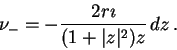
Kvantovací předpis (5) mírně pozměníme. V jednotlivých souřadnicích
zavádíme operátory
Na varietách s netriviální topologií jako je sféra se navíc požaduje, aby operátory
![]() (17) byly úzce svázány. Přesněji, v našem konkrétním
příkladě budeme požadovat, aby existovala funkce
(17) byly úzce svázány. Přesněji, v našem konkrétním
příkladě budeme požadovat, aby existovala funkce ![]() definovaná
a všude nenulová na oblasti
definovaná
a všude nenulová na oblasti ![]() ,
, ![]() (ekvivalentně
(ekvivalentně
![]() ,
, ![]() ) s vlastností
) s vlastností
Rovnost (18) můžeme přepsat jako
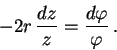
Vyjádříme vektorová pole ![]() příslušná funkcím
příslušná funkcím
![]() (13). Zřejmě
(13). Zřejmě
Místo
![]() budeme psát jednoduše
budeme psát jednoduše
![]() .
Výpočet je opět přímočarý s využitím rovností (17), (15) a
dává
.
Výpočet je opět přímočarý s využitím rovností (17), (15) a
dává
Operátory (23) je opět třeba redukovat. V tomto případě invariantní
podprostor bude tvořen holomorfními funkcemi. Transformační vztah (19)
a tvar funkce ![]() (21) ale představují silné omezení.
Je-li
(21) ale představují silné omezení.
Je-li ![]() holomorfní funkce na
holomorfní funkce na
![]() , potom
, potom
![]() musí být rovněž holomorfní funkce na
musí být rovněž holomorfní funkce na
![]() včetně bodu
včetně bodu ![]() (to jest
(to jest
![]() ). Tato podmínka je splněna právě tehdy, je-li
). Tato podmínka je splněna právě tehdy, je-li ![]() polynom stupně nejvýše
polynom stupně nejvýše ![]() .
.
Ve výsledných vzorečcích vypustíme index ![]() . Pro dané
. Pro dané
![]() operátory
operátory
Metodu orbit, kterou jsme ilustrovali na jednom specielním příkladu, lze aplikovat na libovolnou Lieovu grupu. Pro mnohé běžně používané Lieovy grupy tato konstrukce dává vynikající výsledky a vede na všechny či ``skoro všechny'' irreducibilní reprezentace. Pro některé specielní podtřídy Lieových grup je tento výsledek dokázán rigorózně. Zcela obecné a univerzální tvrzení tohoto typu, pokud je mi známo, neexistuje.