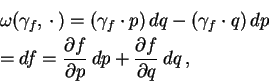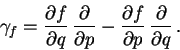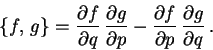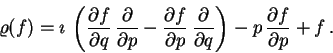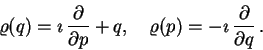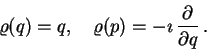


Next: Metoda orbit
Up: Geometrické kvantování
Previous: Geometrické kvantování
Obsah
Buď
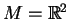 se souřadnicovými funkcemi
se souřadnicovými funkcemi 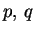 a
a
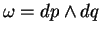 .
Zvolme
.
Zvolme 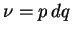 . Vektorové pole
. Vektorové pole 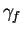 je určeno vztahy
je určeno vztahy
a tedy
Poissonova závorka je dána předpisem (2),
Geometrické kvantování (5) vede na operátory
Specielně,
Jak bylo předesláno, prostor, ve kterém působí operátory
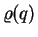 a
a
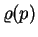 ,
lze redukovat. V tomto jednoduchém případě se řešení nabízí samo. Oba operátory
komutují s derivací
,
lze redukovat. V tomto jednoduchém případě se řešení nabízí samo. Oba operátory
komutují s derivací
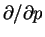 a tedy podprostor funkcí, které
splňují
a tedy podprostor funkcí, které
splňují
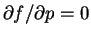 (nezávisí na souřadnici
(nezávisí na souřadnici 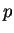 ), je
invariantní. Po této redukci dostáváme všem dobře známé operátory
), je
invariantní. Po této redukci dostáváme všem dobře známé operátory
Je třeba ale zdůraznit, že tuto redukci lze uplatnit pouze na určitou podtřídu
operátorů, specielně na
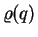 a
a
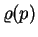 , nikoli však obecně
na operátor
, nikoli však obecně
na operátor
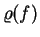 příslušný zcela libovolné funkci
příslušný zcela libovolné funkci 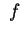 .
.
Pavel Stovicek
2000-02-25
![]() se souřadnicovými funkcemi
se souřadnicovými funkcemi ![]() a
a
![]() .
Zvolme
.
Zvolme ![]() . Vektorové pole
. Vektorové pole ![]() je určeno vztahy
je určeno vztahy