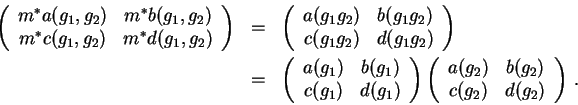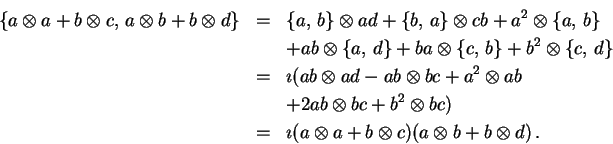


Next: Hopfovy algebry
Up: Poissonovy grupy
Previous: Poissonovy grupy
Obsah
Prvky 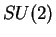 jsou unimodulární matice
jsou unimodulární matice
Unitarita
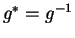 znamená, že
znamená, že
Na 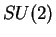 zavedeme funkce
zavedeme funkce
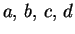 předpisem
předpisem
Tyto funkce nejsou nezávislé, splňují vztahy
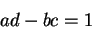 |
(26) |
a
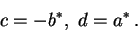 |
(27) |
Zde symbol 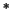 značí involuci v prostoru komplexních funkcí
značí involuci v prostoru komplexních funkcí
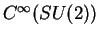 (stejně tak jako v případě libovolné jiné variety) definovanou přirozeně takto:
(stejně tak jako v případě libovolné jiné variety) definovanou přirozeně takto:
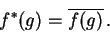 |
(28) |
Často je výhodné omezit se na podalgebru algebry
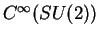 (násobení
funkcí se zavádí samozřejmě bodově jako
(násobení
funkcí se zavádí samozřejmě bodově jako
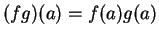 ) generovanou
funkcemi
) generovanou
funkcemi
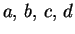 . Tuto podalgebru můžeme popsat jako faktoralgebru
. Tuto podalgebru můžeme popsat jako faktoralgebru
![\begin{displaymath}
% latex2html id marker 710
\AA =\ensuremath{\mathbb {C}}[a,b,c,d]/\mbox{relace (\ref{det}), (\ref{ast})}
\end{displaymath}](img203.gif) |
(29) |
(
![\( \ensuremath{\mathbb {C}}[x,y,\dots ] \)](img204.gif) značí algebru komplexních polynomů v
proměnných
značí algebru komplexních polynomů v
proměnných 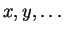 ). Poissonova závorka je předepsána na generátorech
). Poissonova závorka je předepsána na generátorech
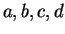 následujícím způsobem
následujícím způsobem
Další rovnosti plynou z relací (27) a z toho, že Poissonova závorka
je reálná, to jest že platí
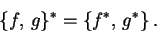 |
(30) |
Jako ukázku ověříme rovnost
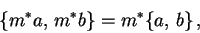 |
(31) |
kde
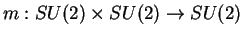 je grupové násobení.
je grupové násobení.
Nejprve si všimněme, že pro libovolné variety 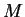 a
a 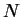 lze přirozeně
vnořit
lze přirozeně
vnořit
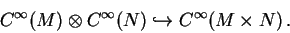 |
(32) |
Jsou-li dány funkce
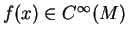 a
a
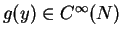 , pak
jejich tenzorový součin
, pak
jejich tenzorový součin 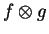 můžeme chápat jako funkci na varietě
můžeme chápat jako funkci na varietě
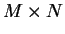 :
:
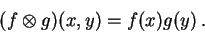 |
(33) |
Tento fakt využijeme i v dalších kapitolách.
Určeme
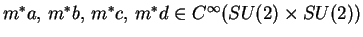 .
Platí
.
Platí
S využitím vnoření (32), (33) můžeme psát
Povšimněme si, že
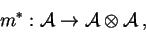 |
(35) |
kde algebru 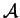 jsme zavedli v (29).
jsme zavedli v (29).
Levá strana (31) je podle pravidla (25) rovna
Poslední výraz se ale rovná pravé straně (31).



Next: Hopfovy algebry
Up: Poissonovy grupy
Previous: Poissonovy grupy
Obsah
Pavel Stovicek
2000-02-25
![]() jsou unimodulární matice
jsou unimodulární matice
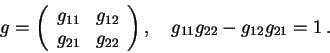
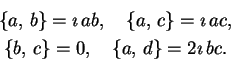
![]() a
a ![]() lze přirozeně
vnořit
lze přirozeně
vnořit
![]() .
Platí
.
Platí