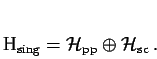Buď ![]() Hilbertův prostor. Zobrazení
Hilbertův prostor. Zobrazení
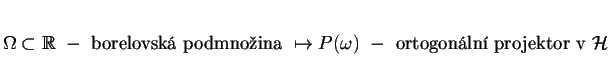
se nazývá projekční mírou, jestliže splňuje
-
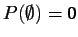 ,
,
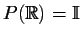 ,
,
- pro vzájemně disjunktní množiny
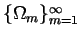 platí
platí
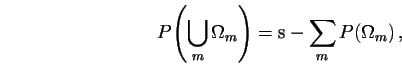
-
Připomeňme základní pojmy týkající se spektrální analýzy samosdružených operátorů.
Buď ![]() Hilbertův prostor. Zobrazení
Hilbertův prostor. Zobrazení
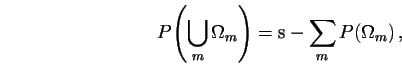
Následující věta představuje dalekosáhlé zobecnění věty o diagonalizaci hermitovských matic a týká se všech samosdružených operátorů v jistém Hilbertově prostoru včetně neomezených.
Existuje vzájemně jednoznačný vztah mezi samosdruženými operátory
![]() na Hilbertově prostoru
na Hilbertově prostoru ![]() a projekčními mírami
a projekčními mírami
![]() na
na ![]() s hodnotami v
s hodnotami v ![]() . Vztah je dán
rovností
. Vztah je dán
rovností
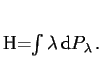
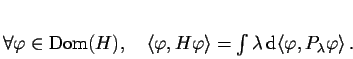
Pro vektor ![]() normovaný k 1 je
normovaný k 1 je
![]() pravděpodobnostní míra na
pravděpodobnostní míra na ![]() určená distribuční funkcí
určená distribuční funkcí
![]() .
.
Připomeňme dále dělení spektra ![]() samosdruženého
operátoru
samosdruženého
operátoru ![]() . Ukazuje se, že pro samosdružené operátory
je účelnější rozkládat přímo Hilbertův prostor
. Ukazuje se, že pro samosdružené operátory
je účelnější rozkládat přímo Hilbertův prostor ![]() než
množinu
než
množinu ![]() . Při té příležitosti poznamenejme,
že atomy projekční míry jsou právě vlastní čísla
. Při té příležitosti poznamenejme,
že atomy projekční míry jsou právě vlastní čísla ![]() ,
neboť platí
,
neboť platí
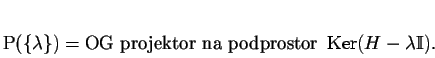
Bodové spektrum
![]() je tvořeno vlastními
hodnotami operátoru
je tvořeno vlastními
hodnotami operátoru ![]() . Označme
. Označme

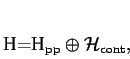
Zúžený operátor
![]() má čistě bodové
spektrum v tom smyslu, že v podprostoru
má čistě bodové
spektrum v tom smyslu, že v podprostoru
![]() existuje ortogonální báze tvořená výhradně vlastními vektory
operátoru
existuje ortogonální báze tvořená výhradně vlastními vektory
operátoru ![]() . Na druhé straně podprostor
. Na druhé straně podprostor
![]() odpovídající spojitému spektru je charakterizován vlastností
odpovídající spojitému spektru je charakterizován vlastností
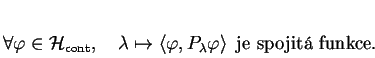
Spektrum lze dále dělit vzhledem ke vztahu k Lebesgueově míře,
kterou označíme symbolem
![]() . Každá borelovská
míra
. Každá borelovská
míra
![]() na
na ![]() se jednoznačně rozkládá
na absolutně spojitou část vzhledem k
se jednoznačně rozkládá
na absolutně spojitou část vzhledem k
![]() ,
píšeme
,
píšeme
![]() , a na
část
, a na
část
![]() singulární s
singulární s
![]() (má nosič na množině Lebesgueovy míry nula). Absolutně spojitou
část můžeme vyjádřit pomocí Lebesgueovy míry jako
(má nosič na množině Lebesgueovy míry nula). Absolutně spojitou
část můžeme vyjádřit pomocí Lebesgueovy míry jako
![]() ,
kde hustota
,
kde hustota ![]() je tzv. Radonova-Nikodymova
derivace (
je tzv. Radonova-Nikodymova
derivace (
![]() ).
).
Podprostor
![]() odpovídající spojitému spektru
operátoru
odpovídající spojitému spektru
operátoru ![]() se dále rozkládá na ortogonální součet
se dále rozkládá na ortogonální součet
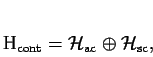
Konečně položme