A) Zesílení metody KAM

Další: B) Poruchová teorie Výš: 7. Vlastní výsledky Předchozí: 7. Vlastní výsledky

A) Zesílení metody KAM

V článku [13] byla použita kombinace metody KAM a adiabatických metod, což umožnilo nahradit podmínku na regularitu operátorové funkce $V(t)$ podmínkou na hladkost této funkce. Článek obsahuje rovněž některá další zesílení a zjednodušení.

Podrobněji, při značení z předcházející kapitoly část B) (viz vztah (c) pro Floquetův hamiltonián) předpokládáme, že spektrum neporušeného hamiltoniánu $H_{0}$ je prosté, diskrétní a splňuje růstovou podmínku $E_{n+1}-E_{n}\geq c\, n^{\alpha }$ , $c\geq 0$ , $\alpha >0$ . Položme

$\begin{displaymath} N(\alpha )=[\tau (\alpha )]+\left[ \frac{\tau (\alpha )}{\alpha +1}\right] +2\, ,\end{displaymath}$

kde

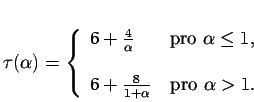
$\begin{displaymath} % latex2html id marker 1425\tau (\alpha )=\left\{ \begin{a... ...{8}{1+\alpha }\quad \textrm{pro }\alpha >1. \end{array}\right. \end{displaymath}$

Je-li $V(t)\in C^{N(\alpha )}$ , potom platí tvrzení KAM věty tak, jak bylo nastíněno v předcházející kapitole.

V další práci [14] byly tyto výsledky dále zobecněny. Zde se vychází z Floquetova hamiltoniánu zapsaného ve tvaru

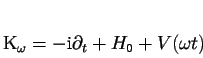
$\begin{displaymath} % latex2html id marker 1426K_{\omega }=-\mathrm{i}\partial _{t}+H_{0}+V(\omega t)\end{displaymath}$

(bez explicitně vyznačené vazebné konstanty). Opět předpokládáme, že spektrum operátoru $H_{0}$ je diskrétní, ale připouští se konečně degenerované vlastní hodnoty. Buď $M_{m}$ násobnost vlastní hodnoty $E_{m}$ . Růstová podmínka je přepsána v poněkud obecnějším tvaru, a sice požadujeme, aby

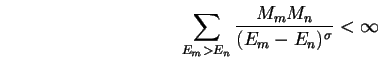
$\begin{displaymath} \sum _{E_{m}>E_{n}}\frac{M_{m}M_{n}}{(E_{m}-E_{n})^{\sigma }}<\infty \end{displaymath}$

pro jisté $\sigma >0$ . Pro měření regularity časově závislé poruchy $V$ byla zvolena vhodná norma označená symbolem $% latex2html id marker 1081 $ \varepsilon _{V} $$ .

Podle hlavní věty za těchto předpokladů ke každému omezenému intervalu $\Omega _{0}$ obsaženému v kladné polopřímce existují dvě kladné konstanty $% latex2html id marker 1083 $ \varepsilon _{\ast } $$ a $% latex2html id marker 1084 $ \delta _{\ast } $$ s vlastností: jestliže $% latex2html id marker 1085 $ \varepsilon _{V}<\varepsilon _{\ast } $$ , potom existuje podmnožina $\Omega _{\infty }\subset \Omega _{0}$ (nerezonančních frekvencí), jejíž Lebesgueova míra splňuje odhad $% latex2html id marker 1087 $ \vert\Omega _{\infty }\vert\geq \vert\Omega _{0}\vert-\delta _{\ast }\varepsilon _{V} $$ , a Floquetův hamiltonián $K_{\omega }$ má čistě bodové spektrum pro každé $\omega \in \Omega _{\infty }$ .

Norma $% latex2html id marker 1090 $ \varepsilon _{V} $$ byla zvolena tak, že v konkrétních vyšetřených modelech je konečná, pokud je operátorová funkce $V$ dostatečně hladká. Přitom požadovaný řád hladkosti byl podstatně snížen oproti výsledku z předcházejícího článku.

Další: B) Poruchová teorie Výš: 7. Vlastní výsledky Předchozí: 7. Vlastní výsledky

Pavel Stovicek
2003-03-26