B) Poruchová teorie pro vlastní hodnoty z hustého bodového spektra

Další: Literatura Výš: 7. Vlastní výsledky Předchozí: A) Zesílení metody KAM

B) Poruchová teorie pro vlastní hodnoty z hustého bodového spektra

Buď $K_{0}$ Floquetův hamiltonián odpovídající neporušenému Hamiltonovu operátoru $H_{0}$ , tedy

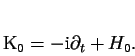
$\begin{displaymath} % latex2html id marker 1428K_{0}=-\mathrm{i}\partial _{t}+H_{0}.\end{displaymath}$

Floquetův operátor pro časově závislý systém pišme ve tvaru

$\begin{displaymath} K_{\beta ,\omega }=K_{0}+\beta \, V(\omega t)\, .\end{displaymath}$

Podle předpokladu spektrum obou částí $K_{0}$ , máme na mysli operátory $% latex2html id marker 1095 $ -\mathrm{i}\partial _{t} $$ a $H_{0}$ , je diskrétní. Platí

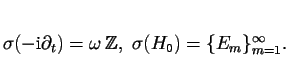
$\begin{displaymath} % latex2html id marker 1430\sigma (-\mathrm{i}\partial _{t... ... \mathbb{Z},\textrm{ }\sigma (H_{0})=\{E_{m}\}^{\infty }_{m=1}.\end{displaymath}$

Spektrum $K_{0}$ je čistě bodové, množina vlastních hodnot je rovna

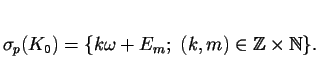
$\begin{displaymath} % latex2html id marker 1431\sigma _{p}(K_{0})=\{k\omega +E_{m};\textrm{ }(k,m)\in \mathbb{Z}\times \mathbb{N}\}.\end{displaymath}$

Příčinou problému malých dělitelů je, že mezi vlastními čísly $K_{0}$ můžeme nalézt mnoho dvojic čísel ležících blízko sebe. V procesu diagonalizace se totiž v některých výrazech objevují rozdíly vlastních čísel jako jmenovatelé.

Tvrzení

Pro skoro všechna $% latex2html id marker 1099 $ \omega \in \mathbb{R}$$ je množina $\sigma _{p}(K_{0})$ hustá v $% latex2html id marker 1101 $ \mathbb{R}$$ .

Zvolme pevně jednu vlastní hodnotu

$\begin{displaymath} F_{k,m}=k\omega +E_{m}\end{displaymath}$

operátoru $K_{0}$ . Položme si otázku, zda existuje a pokud ano, tak v jakém smyslu, poruchová teorie vzhledem k parametru $\beta$ .

Připomeňme nejprve základní výsledek standardní poruchové teorie, která se týká případu, kdy vlastní hodnota je jednoduchá a izolovaná (je izolovaným bodem spektra neporušeného operátoru). V tomto případě píšeme porušený operátor ve tvaru

$\begin{displaymath} H_{\beta }=H_{0}+\beta \, V\end{displaymath}$

a volíme pevně vlastní hodnotu $E_{0}\in \sigma (H_{0})$ . O poruše $V$ předpokládáme pouze, že jde o omezený operátor. Formální řešení rovnice na vlastní hodnotu operátoru $H_{\beta }$ vede na Rayleigh-Schrödingerovu poruchovou řadu

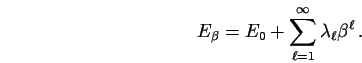
$\begin{displaymath} E_{\beta }=E_{0}+\sum ^{\infty }_{\ell =1}\lambda _{\ell }\beta ^{\ell }\, .\end{displaymath}$

Matematický přesný výsledek lze zformulovat takto.

Věta (Rellich 1937, Kato 1966)

Nechť $E_{0}$ je jednoduchá a izolovaná vlastní hodnota operátoru $H_{0}$ . Potom existuje okolí $U$ bodu $E_{0}$ v komplexní rovině a $% latex2html id marker 1111 $ \delta >0 $$ tak, pro každé $% latex2html id marker 1112 $ \beta \in \mathbb{C}$$ , $% latex2html id marker 1113 $ \vert\beta \vert<\delta $$ , Rayleigh-Schrödingerovu řada absolutně konverguje a okolí $U$ obsahuje právě jeden bod ze spektra operátoru $H_{\beta }$ , kterým je vlastní hodnota $E_{\beta }$ . Příslušný vlastní vektor je rovněž analytickou funkcí komplexní proměnné $\beta$ .

V případě operátoru $K_{\beta ,\omega }$ , ve kterém se parametr $\beta$ uvažuje jako poruchový, je třeba tento výsledek vhodným způsobem modifikovat, neboť vzhledem k hustotě spektra $\sigma (K_{0})$ o vlastní hodnotě $F_{k,m}$ nelze obecně předpokládat, že je izolovaná. Následující věta byla dokázána v článku [15]. Před její formulací uveďme ještě vzorečky pro první dva koeficienty Rayleigh-Schrödingerovy řady.

Buď $f_{k,m}$ vlastní vektor $K_{0}$ příslušný vlastní hodnotě $F_{k,m}$ , $P_{k,m}$ ortogonální projektor na $% latex2html id marker 1126 $ \mathbb{C}f_{k,m} $$ , $% latex2html id marker 1127 $ Q_{k,m}=\mathbb{I}-P_{k,m} $$ a $% latex2html id marker 1128 $ \widehat{K}_{k,m}=Q_{k,m}K_{\beta ,\omega }Q_{k,m} $$ zúžení operátoru $K_{\beta ,\omega }$ na podprostor $% latex2html id marker 1130 $ \mathop\mathrm{Ran}Q_{k,m} $$ . Platí

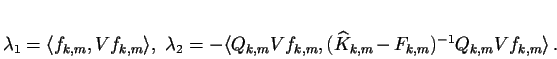
$\begin{displaymath} % latex2html id marker 1435\lambda _{1}=\langle f_{k,m},Vf... ...,m},(\widehat{K}_{k,m}-F_{k,m})^{-1}Q_{k,m}Vf_{k,m}\rangle \, .\end{displaymath}$

Není-li vlastní hodnota $F_{k,m}$ izolovaná, potom například není vůbec zřejmé, že koeficient $\lambda _{2}$ je dobře definovaný, neboť redukovaná rezolventa $% latex2html id marker 1133 $ (\widehat{K}_{k,m}-F_{k,m})^{-1} $$ nepředstavuje omezený operátor.

Věta ([15])

Předpokládáme, že spektrum operátoru $H_{0}$ splňuje růstovou podmínku (gap condition) s $\alpha >0$ , $V(t)\in C^{\infty }$ v silném smyslu (tuto podmínku lze zjemnit). Potom existuje podmnožina plné Lebesgueovy míry (tj. doplněk má míru 0) $\Omega \subset [\, 0,+\infty [\,$ taková, že pro každé $\omega \in \Omega$ a každý pevně zvolený index $% latex2html id marker 1139 $ (k,m)\in \mathbb{Z}\times \mathbb{N}$$ platí:

Koeficienty $\{\lambda _{\ell }\}^{\infty }_{\ell =1}$ Rayleigh-Schrödingerovy řady jsou dobře definovány.
Je-li navíc $\lambda _{2}\neq 0$ , potom existují podmnožina $% latex2html id marker 1142 $ I\subset \mathbb{R}$$ s vlastností

$\begin{displaymath} % latex2html id marker 1436\lim _{\delta \downarrow 0}\fra... ...\delta \, ]\vert=1\quad (0\textrm{ je bodem hustoty množiny }I)\end{displaymath}$

a funkce $F(\beta )$ definovaná na $I$ takové, že jsou splněny podmínky:
1. pro všechna $\beta \in I$ je $F(\beta )$ vlastní číslo operátoru $K_{\beta ,\omega }$ ,
2. $F_{k,m}+\sum ^{\infty }_{\ell =1}\lambda _{\ell }\beta ^{\ell }$ je asymptotickou řadou funkce $F(\beta )$ .

Poznámka

Rayleigh-Schrödingerovy řada nemusí konvergovat a v obecném případě je nutné ji interpretovat pouze jako formální mocninou řadu. Nicméně pokud vezmeme pouze několik prvních členů řady, dostaneme dobré přiblížení k funkci $F(\beta )$ pro malé hodnoty $\beta$ . Podmínka na asymptotickou řadu totiž znamená, že pro každé $% latex2html id marker 1152 $ \ell \in \mathbb{N}$$ je splněno

$\begin{displaymath} F(\beta )=F_{k,m}+\lambda _{1}\beta +\ldots +\lambda _{\ell }\beta ^{\ell }+O(\vert\beta \vert^{\ell +1}).\end{displaymath}$

Další: Literatura Výš: 7. Vlastní výsledky Předchozí: A) Zesílení metody KAM

Pavel Stovicek
2003-03-26