První český samočinný počítač SAPO

Máme-li za úkol vynásobit dvě přirozená čísla a k dispozici tužku a papír, většina z nás použije algoritmus, který jsme se učili už na základní škole:

47

53

141

235

2491

Přesto ale algoritmů pro násobení existuje velké množství. Kromě algoritmů, které urychlují násobení zpaměti a na papíře, také prozkoumáme efektivní algoritmy pro počítačové násobení.

Násobení v binární soustavě a redundantní binární soustavě není pro člověka běžné. Lidé totiž díky deseti prstům provádějí výpočty v soustavě desítkové, tj. čísla zapisují pomocí mocnin desítky a cifer od 0 do 9. Se soustavou binární ovšem pracuje valná většina počítačů.

1. Binární soustava
   Každé přirozené číslo n lze právě jedním způsobem vyjádřit ve tvaru:
   n = a_k2^k + a_k-12^k-1 + ... + a₁2¹ + a₀2⁰,
   kde koeficienty a_k, a_k-1, ..., a₁, a₀ nabývají hodnot nula nebo jedna. Řetězci a_k a_k-1 ... a₁ a₀ říkáme binární zápis čísla n. Připomeňme, že binární zápis se získá hladovým algoritmem:
   • Chceme-li najít binární zápis čísla 13, podíváme se, jakou nejvyšší mocninu dvojky číslo 13 obsahuje. To je 8.
   • Poté od 13 odečteme 8 a pro získaný rozdíl 5 opět najdeme největší mocninu dvojky, kterou číslo 5 obsahuje. To je 4.
   • Na závěr spočteme rozdíl 5 - 4 = 1, a to je nultá mocnina dvojky.
   • Získáme 13 = 8 + 4 + 1, a tedy číslo 13 má v binární soustavě zápis 1101.
   Násobení v binární soustavě je velmi podobné jako nám známé klasické násobení v desítkové soustavě. Například číslo 11 s binárním zápisem 1011 a číslo 5 s binárním zápisem 101 se vynásobí následujícím způsobem:
   
   Výsledek je 32 + 16 + 4 + 2 + 1 = 55. Všimněme si, že rychlost násobení odpovídá počtu jedniček v binárním zápisu násobitele (v našem případě jsou dvě jedničky v binárním zápisu 5), právě tolik sčítání totiž musíme provést.
   Program na binární násobení.
2. Redundantní binární soustava
   Připusťme nyní v binární soustavě cifry -1, 0 a 1. Zápisy čísel už nejsou jediné možné, soustava je redundantní. Například 15 = 8 + 4 + 2 + 1 a taky 15 = 16 - 1, tedy jak 1111 tak i 10001 jsou zápisy 15 v redundantní binární soustavě. Vyberme zápis s maximálním počtem nul. K tomu stačí aplikovat následující přepisovací pravidla, dokud je co přepisovat:

   01111 → 10001

   01111 → 10001

   11 → 01

   11 → 01

   Zatímco průměrný počet nul ve standardním binárním zápisu je 1/2, v redundantním binárním zápisu s maximálním možným počtem nul jsou to 2/3. Jelikož je rychlost násobení úměrná počtu nul, je jasné, že redundantní binární soustava je pro násobení velkých čísel výhodnější. Na závěr ještě poznamenejme, že násobíme analogicky jako v klasické binární soustavě. Pouze u znamének dáváme pozor: při násobení cifer stejného znaménka má výsledek znaménko plus, při násobení cifer opačného znaménka má výsledek znaménko mínus. Tedy například násobení 11 a 5 proběhne následovně:
   
   Výsledek je tedy 64 - 8 - 1 = 55.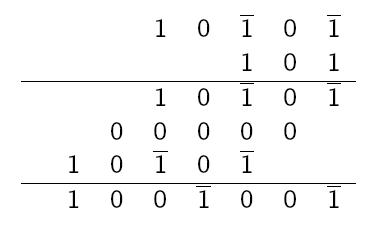

Program na násobení v redundantní binární soustavě.

Klasické násobení označuje násobení dvou přirozených čísel zadaných pomocí zápisů v bázi b, kde b je přirozené číslo větší nebo rovno 2. Binární zápis (b = 2) a desítkový zápis (b = 10) jsou speciální případy zápisu čísel v bázi b s ciframi 0, 1, ..., b-1.

• Soustava s přirozeným základem
  Každé přirozené číslo n lze právě jedním způsobem vyjádřit ve tvaru:
  n = a_kb^k + a_k-1b^k-1 + ... + a₁b¹ + a₀b⁰,
  kde koeficienty a_k, a_k-1, ..., a₁, a₀ nabývají hodnot 0, 1, ..., b-1. Řetězci a_k a_k-1 ... a₁ a₀ říkáme zápis čísla n v soustavě se základem b. Připomeňme, že takový zápis se získá hladovým algoritmem:
  • Chceme-li najít zápis čísla n v bázi b, podíváme se, jakou nejvyšší mocninu b^k číslo n obsahuje a kolikrát ji obsahuje. To bude koeficient a_k, který je jistě menší než b.
  • Poté od n odečteme a_kb^k a pro získaný rozdíl opět najdeme největší mocninu b^j, kterou obsahuje, a jako a_j označíme počet výskytů b^j v rozdílu.
  • Všechny koeficienty mezi a_j a a_k (pokud nějaké takové jsou, tj. pokud je j menší než k-1) jsou nulové. Analogicky pokračujeme dále.
  Popišme nejprve algoritmus klasického násobení tak, jak by jej provedl počítač, a poté jej porovnejme s algoritmem "tužky a papíru".
• Algoritmus M (multiplication)
  Násobíme přirozená čísla U,V, kde u_n-1 ... u₁u₀ je zápis U v bázi b a v_m-1 ... v₁v₀ je zápis V v bázi b. Označme W = U × V. Snadno si rozmyslíme, že délka zápisu W v bázi b bude maximálně m+n. Označme w_m+n-1 ... w₁w₀ zápis W.
  1. Inicializace W a i , j   Polož w_n-1 = ... = w₁ = w₀ a i = 0 a j = 0.
  2. Násobení nulou   Pokud v_j = 0, pak polož w_i+j = 0 a jdi na krok 6.
  3. Inicializace i   Polož i = 0, k = 0.
  4. Násob a sečti   Polož t = u_i × v_j + w_i+j + k. Pak polož w_i+j = t mod b a k = [t/b], kde [x] je největší celé číslo, které je menší nebo rovno x a t mod b = t-b[t/b] (zbytek po celočíselném dělení).
  5. Cyklus na i   Polož i:= i + 1. Pokud i < n, jdi na krok 4. Jinak polož w_i+j = k.
  6. Cyklus na j   Polož j := j + 1. Pokud j < m, jdi na krok 2. Jinak konec.
  Ilustrujme algoritmus M pro b = 10 a W = U × V, kde U=914=u₂u₁u₀ a V=84=u₁u₀.
  
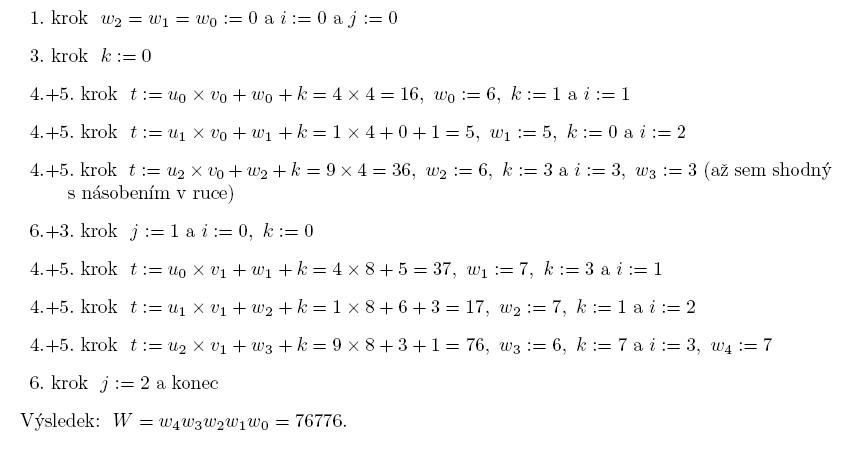
• Algoritmus M versus násobení na papíře
  Při násobení na papíře tvoříme částečné součiny, které příslušně posunuté vlevo sepisujeme pod sebe a na závěr vysčítáme. Na počítači je výhodnější provádět násobení a sčítání současně - tak postupuje algoritmus M. Není těžké si rozmyslet, že t nabývá hodnot 0, 1, ..., b²-1 a přenos (carry) k nabývá hodnot 0, 1, ..., b-1, proto víme, jak velké registry potřebujeme pro implementaci. Počítače navíc pracují s bází 2, krok 2 tedy ušetří práci, nastává průměrně v polovině případů. (Už z předchozí sekce víme, že v binární soustavě je rychlost násobení úměrná počtu nul v binárním zápisu násobitele.) Nevýhodou klasického algoritmu je jeho pomalost. Už pro m = n = 4 je možné násobit U × V rychleji.
• Složitost algoritmu M pro bázi b = 2
  Definujme nejprve elementární operace:
  1. součet a rozdíl 1-bitových čísel a případně přenos,
  2. součin dvou 1-bitových čísel s 2-bitovým výsledkem,
  3. celočíselné dělení 2-bitového čísla 1-bitovým za předpokladu, že kvocient i zbytek výsledku jsou 1-bitové.
  Počet takových operací udává složitost algoritmu. V případě algoritmu M lze dokázat, že složitost násobení čísel s délkami binárních rozvojů m a n je O(m.n), tj. existuje konstanta K>0 taková, že pro libovolná dvě přirozená čísla je složitost jejich násobení algoritmem M menší než K.m.n, kde m a n jsou délky jejich binárních rozvojů.
  nahoru

  Rychlé násobení je násobení se složitostí menší než násobení klasické. Snaha o zrychlení algoritmů se zesiluje ruku v ruce s rozvojem počítačů a speciálně snaha o maximální zrychlení násobení je dána potřebami kryptografie, kde je nutné násobit v přijatelném čase ohromná čísla (řádově 10¹⁰⁰). My popíšeme dvě rychlá násobení - Karacubovo násobení a Schönhageovo násobení v modulární aritmetice - založená na důvtipných myšlenkách a poměrně jednoduše popsatelná. Mezi rychlými algoritmy patří k těm nejstarším, ovšem algoritmy ještě rychlejší už jsou příliš technické.

  Zájemce o násobení přirozených čísel s binárním rozvojem délky n blížící se svou složitostí libovolně blízko až k nejnižší hranici O(n) si dohledá podrobnosti v D. E. Knuth, The Art of Computer Programming volume 2: Seminumerical Algorithms, 3rd ed, Addison-Wesley Boston etc., 1998. Poznamenejme, že jde o jednu z nejrespektovanějších publikací v oboru programování. Donald E. Knuth (na obrázku) je průkopníkem oboru matematické algoritmické analýzy a významnou osobností v mnoha dalších oborech teoretické počítačové vědy.
  nahoru

  Karacubovo násobení vyvrátilo domněnku, že složitost násobení dvou přirozených čísel s binárním rozvojem délky n je O(n²). Tento názor razil ještě v roce 1960 na semináři moskevské univerzity zakladatel teorie složitosti algoritmů Andrej N. Kolmogorov (na obrázku).

  Semináře se účastnil jeho student Anatolij A. Karacuba, který navrhl a o dva roky později publikoval důvtipný algoritmus s nižší složitostí. Popíšeme algoritmus, který je založen na stejné myšlence jako původní Karacubův, ale je ještě trochu jednodušší. Chceme násobit dvě 2n-bitová čísla U s binárním zápisem u_2n-1...u₁u₀ a V s binárním zápisem v_2n-1...v₁v₀.
  • Zapíšeme U, V následujícím způsobem U = 2ⁿU₁ + U₀ a V = 2ⁿV₁ + V₀. Platí tedy, že U₁ má binární zápis u_2n-1...u_n a U₀ má zápis u_n-1...u₁u₀, podobně V₁ má binární zápis v_2n-1...v_n a V₀ má zápis v_n-1...v₁v₀.
  • Následující formule redukuje problém na 3 násobení n-bitových čísel, několik sčítání, resp. odečítání a posouvání binární čárky:
    U×V = (2²ⁿ+2ⁿ)U₁V₁+2ⁿ(U₁-U₀)(V₀-V₁)+(2ⁿ+1)U₀V₀.
  Ilustrujme Karacubův algoritmus pro U × V, kde U=210 a V=119. Binární zápis U je 11010010 a binární zápis V je 01110111.
  
  Není těžké dokázat, že složitost Karacubova násobení je O(n^log₂3). Platí log₂3 je přibližně 1,5849, což je číslo menší než 2, a tedy jde skutečně o rychlé násobení podle naší definice.
  Adaptací na desítkovou soustavu lze převést násobení 8-místných čísel na násobení čísel 4-místných, které už dobří počtáři zvládnou zpaměti. Kupodivu se nezdá, že by taková metoda byla známa před rokem 1962 a že by ji tedy používali "zázrační počtáři", kteří v minulosti bavili obecenstvo násobením obrovských čísel.
  nahoru

  Schönhageovo násobení v modulární aritmetice sice není rychlejší než Karacubův algoritmus, ale je založeno na odlišných myšlenkách a na neobvyklé reprezentaci čísel, takže je rozhodně zajímavé do jeho tajů proniknout.

  Jeho základním stavebním kamenem je modulární aritmetika, u jejíhož zrodu stáli čeští vědci Antonín Svoboda (tvůrce prvního československého počítače SAPO a velmi významný průkopník informatiky nejen u nás - o jeho klikatých osudech se dočtete v článku Petra Vysokého 100 let od narození Antonína Svobody a jeho podobu vidíte na obrázku) a Miroslav Valach. Nezávisle na nich přišel se stejnou myšlenkou také L. H. Garner.
  1. Modulární zápis
     Dosud jsme se seznámili jen se zápisy přirozených čísel v pozičních soustaváchch s přirozenou bází (případně jsme připustili záporné cifry). Nyní přijde naprosto odlišný zápis přirozených čísel.
     Nechť jsou dána přirozená čísla m₁, m₂, ..., m_r. Pak modulárním zápisem nezáporného celého čísla U nazveme (u₁,u₂,...,u_r,), kde u_i je rovno U mod m_i pro každé i od 1 do r. Připomeňme, že mod k znamená zbytek po celočíselném dělení číslem k a nabývá hodnot od 0 do k-1. (Například 13=3.4+1, a tedy 13 mod 4=1.) Ukažme si na příkladu takovou modulární reprezentaci.
     
     Aby takový zápis měl smysl, mělo by být možné původní číslo ze znalosti modulární reprezentace zrekonstruovat. To bez dodatečných podmínek možné není. Všimněme si, že čísla 56 a 26 mají stejný modulární zápis (0,2,1). Naštěstí platí následující tvrzení, které je důsledkem známé Čínské zbytkové věty: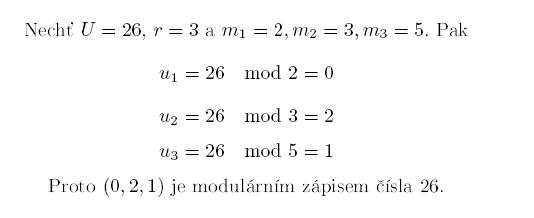
     Nechť a,u₁,u₂,...,u_r jsou nezáporná celá čísla a nechť m₁, m₂, ..., m_r jsou přirozená po dvou nesoudělná čísla. Pak existuje právě jedno U, které splňuje
     1. a <= U < a + m = a + m₁. m₂. ... . m_r,
     2. (u_1,u_2,,...,u_r) je modulární reprezentace U.
     Z této věty plyne, že když se omezíme na čísla od 0 do 2.3.5 = 30, pak mezi nimi právě jen číslo 26 má modulární reprezentaci (0,2,1).
  2. Modulární aritmetika
     V modulární aritmetice je možné paralelizovat sčítání a násobení. Platí totiž, že pokud U a V jsou přirozená čísla s modulárními reprezentacemi (u₁,u₂,...,u_r) a (v₁,v₂,...,v_r) a obě leží mezi 0 a m = m₁. m₂. ... . m_r, pak
     1. U + V má modulární reprezentaci ((u₁+v₁) mod m₁, (u₂+v₂) mod m₂,...,(u_r+v_r) mod m_r),
     2. U x V má modulární reprezentaci ((u₁.v₁) mod m₁, (u₂.v₂) mod m₂,...,(u_r.v_r) mod m_r).
     Nevýhodou je, že při pohledu na modulární reprezentace nepoznáme, které z čísel je větší. Navíc nepoznáme, zda výsledek operace nevypadl z intervalu 0 až m. Proto potřebujeme rychlou konverzi, která číslům přiřazuje modulární zápis a zejména z modulárního zápisu rychle vyrábí zpět reprezentovaná čísla.
  3. Binární modulární aritmetika
     Jak uvidíme, takovou rychlou konverzi poskytuje vhodná volba modulí m₁, m₂, ..., m_r. Následující nápad se zrodil v hlavě A. S. Fraenkela.
     Volme modula m_i= 2^e_i -1, kde e₁ < e₂ < ... < e_r jsou po dvou nesoudělná. Nesoudělnost takových modulí je zaručena následující větou:
     Nechť e, f jsou přirozená čísla. Pak 2^e -1 a 2^f -1 jsou nesoudělná, právě když e a f jsou nesoudělná.
     • Konverze U na (u₁,u₂,...,u_r)
       Zapišme U ve tvaru U = a_tA^t + a_t-1A^t-1 + ... +a₁A + a₀, kde A = 2^e_i. Uvědomme si, že binární zápis a₀ získáme tak, že vezmeme posledních e_i bitů v binárním zápisu U, pro získání a₁ vezmeme předposledních e_i bitů atd. Vlastně jen nasekáme binární zápis U od konce po e_i bitech. Protože A = 1 mod (2^e_i-1), dostaneme u_i = (a_t + a_t-1 + ... + a₀) mod (2^e_i-1).
       V desítkové soustavě máme analogii (tzv. casting out nines - vyloučení devítek)
       789 mod 9 = 7 + 8 + 9 mod 9 = 6, což skutečně platí, protože 789 = 87.9 + 6. Ilustrujme tento algoritmus opět na příkladu.
     
     • Konverze (u₁,u₂,...,u_r) na U
       Je o něco složitější. Probíhá ve dvou krocích:
       • Nejprve je třeba najít r(r-1)/2 konstant c_ij, indexy i,j nabývají hodnot od 1 do r, i < j a platí c_ijm_i=1 mod m_j.
         K tomu využijeme následující algoritmus.
       
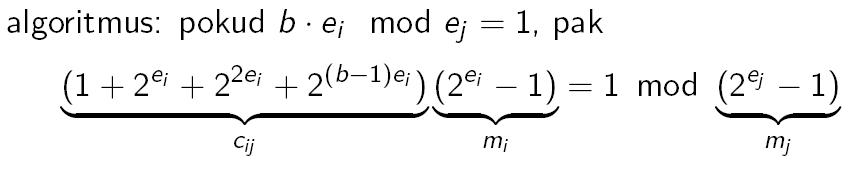
       • Poté položíme U = v_r m_r-1...m₂m₁ +...+ v₃ m₂m₁ + v₂ m₁ + v₁, kde
         v₁ = u₁ mod m₁
         v₂ = (u₂-v₁)c₁₂ mod m₂
         v₃ = ((u₃-v₁)c₁₃-v₂)c₂₃ mod m₃
         ...
         v_r = (((u_r-v₁)c_1r-v₂)c_2r-...)c_r-1r mod m_r
         Snadno se přesvědčíme, že takto spočtené U splňuje
         1. U je nezáporné číslo menší než m,
         2. U mod m_i = u_i pro každé i od 1 do r.
         Ilustrujme i tento algoritmus na příkladu.
         
  4. Schönhageovo násobení
     Nyní máme vše připraveno k tomu, abychom pochopili fungování algoritmu, který Arnold Schönhage v roce 1966 navrhl. Nejprve si všimněme, jak šikovně volí 6 modulí, která budou v jeho algoritmu vystupovat.
     
     Pro posloupnost q₀=1 a q_k=3q_k-1-1, tj. q_k=(3^k+1)/2 pro každé k přirozené, jsou modula po dvou nesoudělná. Navíc platí, že při násobení p_k=(18q_k+8)-bitových čísel nedojde k přetečení, tj. zůstaneme mezi 0 a m=m₁. m₂. ... . m₆, protože m je větší než 2^2p_k.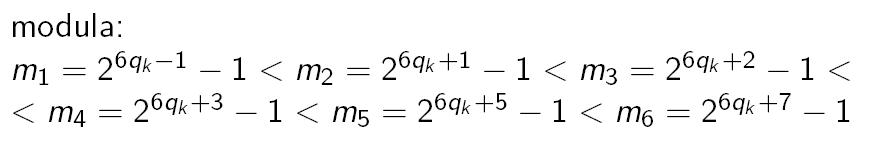
     Teď již samotný Schönhageův algoritmus. Chceme násobit přirozená čísla U a V, označme W = U x V. Najdeme nejmenší p_k tak, že násobená čísla jsou nejvýše p_k-bitová. K p_k najdeme příslušná modula.
     
     Všimněme si, že algoritmus převádí úlohu násobit p_k-bitová čísla na násobení p_k-1-bitových čísel. To je podobná myšlenka jako v Karacubově násobení vedoucí ke snížení složitosti. Tentokrát je možné - i když pracné - dokázat, že složitost Schönhageova násobení je O(n^log₃6). Platí log₃6 je přibližně 1,63, což je číslo menší než 2, a tedy jde opět o rychlé násobení podle naší definice.
  nahoru