V této části předpokládáme, že hamiltonián ![]() nezávisí
na čase.
nezávisí
na čase.
Buďte ![]() samosdružený operátor v
samosdružený operátor v ![]() a
a
![]() operátor relativně kompaktní vzhledem
k
operátor relativně kompaktní vzhledem
k ![]() , to jest
, to jest

Ze Schwarzovy nerovnosti snadno plyne, že vlastnost (a) je důsledkem (b).
RAGE věta připouští geometricko-pravděpodobnostní interpretaci
v případě, kdy Hilbertovým prostorem je
![]() .
Za omezený operátor
.
Za omezený operátor ![]() zvolme ortogonální projektor na
vektory, které popisují stav systému s polohou uvnitř koule
zvolme ortogonální projektor na
vektory, které popisují stav systému s polohou uvnitř koule
![]() se středem v počátku a poloměrem
se středem v počátku a poloměrem ![]() . Přesněji,
. Přesněji,
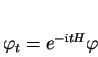
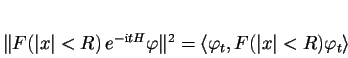
Některé výsledky pro časově nezávislé systémy lze zobecnit na
periodicky časově závislé systémy. Buď ![]() perioda. Evoluční
operátor přes periodu
perioda. Evoluční
operátor přes periodu ![]() se nazývá operátorem
monodromie nebo také Floquetovým operátorem. Buď
se nazývá operátorem
monodromie nebo také Floquetovým operátorem. Buď
![]() jednoparametrická třída omezených operátorů s vlastnostmi
jednoparametrická třída omezených operátorů s vlastnostmi
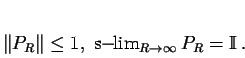
Řekneme, že vektor ![]() patří do třídy
patří do třídy
![]() (volně se šířící stavy), právě když
(volně se šířící stavy), právě když
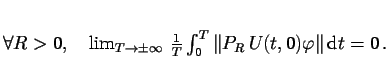
Podmínka na volné stavy je přímým zobecněním podmínky z RAGE
věty. Podmínka na vázané stavy (vzhledem k ![]() ) má rovněž
pravděpodobnostní interpretaci. Pro dostatečně velké hodnoty
) má rovněž
pravděpodobnostní interpretaci. Pro dostatečně velké hodnoty
![]() bude pravděpodobnost nalezení systému ve stavu odpovídajícímu
projektoru
bude pravděpodobnost nalezení systému ve stavu odpovídajícímu
projektoru
![]() malá nezávisle na čase
malá nezávisle na čase ![]() .
.
Předpokládejme, že evoluční operátor ![]() je
je ![]() -periodický
a množina
-periodický
a množina
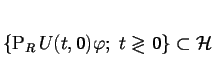
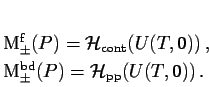
Spektrální teorie pro unitární operátory je zcela analogická spektrální teorii pro samosdružené operátory s tím rozdílem, že spektrum samosdruženého operátoru je obsaženo v reálné přímce zatímco spektrum unitárního operátoru je obsaženo v jednotkové kružnici v komplexní rovině.
Intuitivní rozdělení Hilbertova prostoru na základě geometrického pohledu na volně se šířící a vázané stavy se v tomto případě ukazuje být vhodným, neboť je v přesné korespondenci se spektrálními vlastnostmi operátoru monodromie.