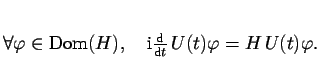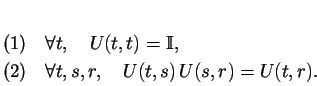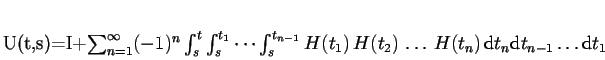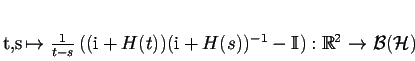

Další: 3. Spektrální rozklad
Výš: Obsah
Předchozí: 1. Úvod
Pro systémy nezávislé na čase je základní větou popisující časový
vývoj
Pro časově závislé systémy hamiltonián závisí na
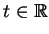 ,
ale stále jde o samosdružený operátor,
,
ale stále jde o samosdružený operátor,
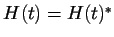 .
Časový vývoj je popsán evolučním operátorem (propagátorem)
.
Časový vývoj je popsán evolučním operátorem (propagátorem)
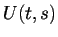 , který nyní závisí na dvou parametrech (
, který nyní závisí na dvou parametrech (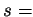 počáteční čas,
počáteční čas, 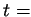 koncový čas). Dostáváme tak zobrazení
koncový čas). Dostáváme tak zobrazení
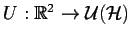 , od kterého se požaduje, aby bylo
silně spojité. Zde symbol
, od kterého se požaduje, aby bylo
silně spojité. Zde symbol
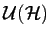 značí grupu unitárních
operátorů na Hilbertově prostoru. Evoluční operátor splňuje následující
podmínky:
značí grupu unitárních
operátorů na Hilbertově prostoru. Evoluční operátor splňuje následující
podmínky:
Rovnice (2) se nazývá někdy Chapman-Kolmogorovova rovnice.
Vztah 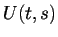 k
k 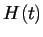 je dán diferenciální rovnicí
je dán diferenciální rovnicí
Je třeba ale určit, v jakém smyslu chápat tuto rovnici.
Periodický časový vývoj je určen hamiltoniánem periodicky závisejícím
na 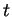 s periodou
s periodou 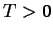 , tj.
, tj.
Pro evoluční operátor to implikuje podmínku
Ve speciálním případě, kdy operátory 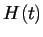 jsou omezené,
lze poměrně snadno dokázat existenci časového vývoje.
jsou omezené,
lze poměrně snadno dokázat existenci časového vývoje.
Věta (Dysonův rozvoj 1949)
Předpokládáme, že
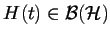 pro všechna
pro všechna
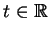 a že zobrazení
a že zobrazení
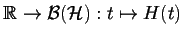 je silně
spojité. Potom
je silně
spojité. Potom
je operátorem časového vývoje a pro všechna
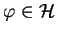 platí
platí
Pro neomezené operátory je třeba naložit další podmínky zaručující
existenci časového vývoje. Standardní ale ne nejslabší možné
postačující podmínky jsou zformulovány v následující větě.
Věta (Kato 1953)
Předpokládejme, že
-
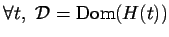 (definiční obor je
časově nezávislý),
(definiční obor je
časově nezávislý),
- zobrazení
lze dodefinovat (pro 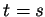 ) jako silně spojitou funkci.
) jako silně spojitou funkci.
Potom existuje právě jeden evoluční operátor 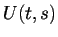 takový,
že
takový,
že


Další: 3. Spektrální rozklad
Výš: Obsah
Předchozí: 1. Úvod
Pavel Stovicek
2003-03-26
![]() ,
,
![]() , v Hilbertově prostoru
, v Hilbertově prostoru ![]() je tvaru
je tvaru
![]() ,
kde
,
kde ![]() je samosdružený (obecně neomezený) operátor.
Naopak, je-li
je samosdružený (obecně neomezený) operátor.
Naopak, je-li ![]() , potom
, potom
![]() je silně spojitá jednoparametrická unitární grupa.
je silně spojitá jednoparametrická unitární grupa.
![]() je invariantní vzhledem
k operátorům
je invariantní vzhledem
k operátorům ![]() ,
,
![]() , a platí
, a platí