Rhindův papyrus	Thoth - egyptský bůh matematiky	Augustin Louis CAUCHY

Máme-li za úkol vynásobit dvě přirozená čísla a k dispozici tužku a papír, většina z nás použije algoritmus, který jsme se učili už na základní škole:

47

53

141

235

2491

Přesto ale algoritmů pro násobení existuje velké množství. Kromě algoritmů, které urychlují násobení zpaměti a na papíře, také prozkoumáme efektivní algoritmy pro počítačové násobení.

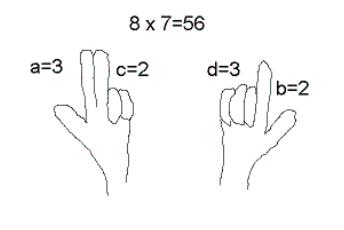
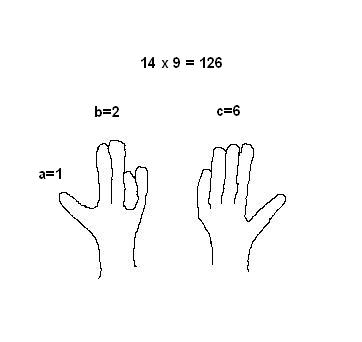
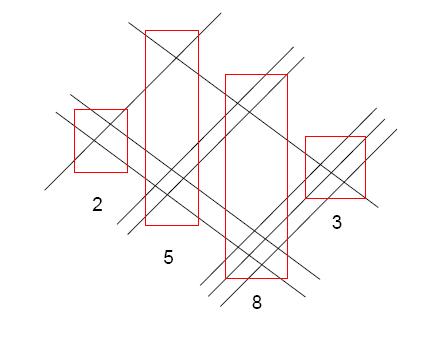
Násobení na prstech paní učitelky na základní škole nevidí rády. Chtějí nás totiž naučit násobit do 10 krát 10 zpaměti "jako když bičem mrská". Přesto je použití prstů přirozeným zjednodušením, kterým si lidé pomáhají při výpočtech odedávna. Středověcí obchodníci s oblibou využívali tzv. cikánskou násobilku, která umožňuje násobit pomocí prstů do 9 krát 9 (se znalostí pouhé malé násobilky do 5 krát 5). Její princip pochopíte z následujícího obrázku.

Pokud chceme násobit 8 krát 7, zeptáme se: "Osm a kolik je deset?" "A dva." Skrčíme dva prsty na první ruce (c = 2). To samé uděláme s číslem sedm. Schováme tedy tři prsty na druhé ruce (d = 3). Na pozici desítek napíšeme součet vztyčených prstů (a + b = 3 + 2 = 5) a na pozici jednotek napíšeme součin skrčených prstů (c . d = 2 . 3 = 6). A obdržíme správný výsledek 56. Bystrý čtenář si snadno rozmyslí, že algoritmus je použitelný jen k násobení čísel, která jsou obě větší než 5, a že funguje díky následujícím rovnostem (a také si všimne, že při násobení některých čísel narazíme na jistá úskalí!)

(10 - c)(10 - d)	=	100 - (c + d)10 + cd
	=	10(10 - c - d) + cd
	=	10(a+b) + cd

Násobení devíti nedělalo středověkým trhovcům problémy ani pro čísla od 12 do 19. Postupovali podle následujícího obrázku. Pokud chceme násobit 14 krát 9, skrčíme na levé ruce čtvrý prst. Zleva pak první prst reprezentuje stovky (a=1), zbylé prsty před skrčeným reprezentují desítky (b=2) a prsty, které následují za skrčeným, reprezentují jednotky (c=6). Výsledek: 126. Snadno si rozmyslíme, že algoritmus funguje, pomocí následujících rovností. Násobíme-li (10+d) krát 9, kde d = 2,...,9, platí:

(10 + d)9	=	90 + 9d
	=	100 + 10(d - 2) + (10 - d)
	=	100a + 10b + c

Čínské (grafické) násobení je velmi názorné.

• Chceme-li čínským způsobem vynásobit 123 krát 21, namalujeme za násobence ve směru z JZ na SV postupně jednu rovnoběžku za stovky, dvě rovnoběžky za desítky a tři rovnoběžky za jednotky. Poté za násobitele namalujeme ze SZ směrem na JV dvě rovnoběžky za desítky a jednu za jednotky.
• Do disjunktních obdélníků uzavřeme průsečíky odpovídající tisícovkám, stovkám, desítkám a jednotkám a zjistíme jejich počty.
• V našem případě máme v prvním obdélníku 2 průsečíky, ve druhém 5, ve třetím 8 a ve čtvrtém 3. Výsledek 2583.

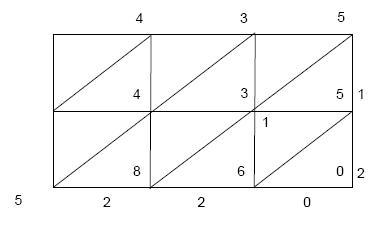
Indické násobení zde popsané není jediné, které se ve staré Indii používalo. Existovalo více než osm rozličných způsobů násobení.

• Chceme-li indickým způsobem vynásobit 435 krát 12, namalujeme tabulku se třemi slouci a dvěma řádky, které označíme ciframi násobence a násobitele.
• Každé okénko tabulky rozdělíme úhlopříčkou na dva trojúhelníky.
• Nyní tabulku vyplníme tak, že pro každou buňku násobíme cifry, které značí, v jakém sloupci a řádku se buňka nachází. Pokud vyjde číslo menší než deset, napíšeme jej do dolního trojúhelníku. Pokud je výsledek větší nebo roven deseti, napíšeme desítky do horního trojúhelníku a jednotky do dolního trojúhelníku.
• Na závěr vysčítáme zprava doleva čísla podél úhlopříček. Jednotky sepisujeme a desítky si pamatujeme a "přenášíme" je. Výsledek je 5220.

Egyptské (etiopské) násobení je založené na binárním zápisu násobence. (Samozřejmě etiopské kmeny nemluvili o binárním zápisu, když Egypťanům svůj způsob násobení vysvětlovali :)

• Chceme-li egyptským způsobem vynásobit 13 krát 15, sestavíme si tabulku, jejíž první sloupec tvoří mocniny dvou menší nebo rovny 13 a druhý sloupec vznikne postupným zdvojováním 15.
• V prvním sloupci si zaškrtneme mocniny dvou, které se vyskytují v binárním zápisu 13.
• Ten zřejmě staří Egypťané sestavili hladovým algoritmem: Podívali se, jakou nejvyšší mocninu dvojky číslo 13 obsahuje. To je 8. Poté od 13 odečetli 8 a pro získaný rozdíl 5 opět našli největší mocninu dvojky, kterou číslo 5 obsahuje. To je 4. Na závěr spočetli rozdíl 5 - 4 = 1, a to je nultá mocnina dvojky. Získali 13 = 1 + 4 + 8.
• Pak již stačilo sečíst ve druhém sloupci řádky odpovídající zaškrtnutým mocninám dvou. Výsledek 195.

A odkud Egypťané věděli, že každé číslo má binární zápis, tj. může být vyjádřeno jako součet mocnin dvou? Pravděpodobně díky rovnoramenným vahám. Ty totiž používali a mohli si tedy všimnout, že mají-li závaží hmotnosti n debenů (základní jednotka staroegyptského systému měření hmotnosti), mohou si pomocí rovnoramenných vah vyrobit závaží hmotnosti 2n debenů tak, že na jednu misku vah položí n-debenové závaží a na druhé misce vah jej vyváží. Spojením použitých předmětů vznikne hledané závaží hmotnosti 2n debenů. Poté již stačilo vypozorovat, že každý předmět hmotnosti m krát n debenů, kde m je přirozené číslo, je možno vyvážit pomocí závaží o hmotnostech n, 2n, 4n, 8n atd.
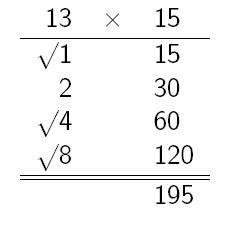
Program na egyptské násobení.

Ruské (sedlácké) násobení je velmi podobné egyptskému. Ještě v 19. století se používalo na ruském venkově a zřejmě tak násobila většina Evropanů před prosazením dnešního indo-arabského způsobu násobení, které se dnes učíme na základní škole.

• Chceme-li ruským způsobem vynásobit 13 krát 15, sestavíme si tabulku, jejíž první sloupec tvoří zbytky po opakovaném celočíselném dělení násobence dvojkou a druhý sloupec vznikne postupným zdvojováním 15.
• Nyní stačí sečíst ve druhém sloupci řádky odpovídající jednotkovým zbytkům. Výsledek 195.

Uvědomte si, že pokud přirozené číslo n není dělitelné dvojkou, znamená to, že na posledním místě v jeho binárním zápisu je jednička. Pokud je dělitelné dvojkou, pak má v binárním zápisu na posledním místě nulu. Snadno si pak rozmyslíte, že binární zápis čísla n lze získat také následujícím algoritmem:

1. Vyděl číslo dvěma.
2. Je-li dělitelné, zapamatuj si nulu a číslo n/2. Není-li dělitelné, zapamatuj si jedničku a číslo (n - 1)/2.
3. Pokud zapamatované číslo není nula, opakuj algoritmus. Pokud zapamatované číslo je nula, binární zápis získáš sepsáním nul a jedniček zleva doprava v pořadí od poslední zapamatované cifry k první.

Program na ruské násobení.

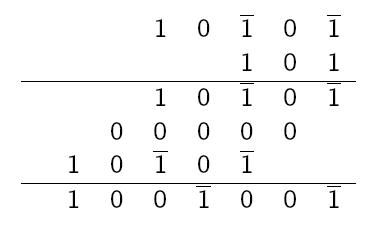
Cauchyovo komplementární násobení využívá zápis čísel pomocí záporných cifer. Všimněme si, že při použití Cauchyova komplementárního násobení si vystačíme s malou násobilkou do 5 krát 5!

• Chceme-li násobit 57 krát 17 Cauchyovým algoritmem, zapíšeme nejprve násobence i násobitele pomocí cifer od -4 do 5, tj. 57 = 143 = 100 - 40 - 3 a 17 = 23 = 20 - 3. Pruhy nad ciframi znamenají, že cifry mají znaménko mínus.
• Poté již násobíme analogicky jako v klasické desítkové soustavě. Pouze u znamének dáváme pozor: při násobení dvou záporných cifer nebo dvou kladných cifer má výsledek znaménko plus, při násobení cifer opačného znaménka má výsledek znaménko mínus.

Abychom mohli Cauchyovo komplementární násobení používat, musíme umět převádět zápisy čísel mezi klasickou desítkovou soustavou a desítkovou soustavou s ciframi od -4 do 5. K takové konverzi slouží následující jednoduchý algoritmus:

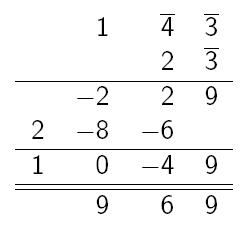
• Chceme-li zapsat 57 v desítkové soustavě s ciframi od -4 do 5, v prvním kroku přičteme 44 (obecně přičteme číslo sestavené z tolika čtyřek kolik cifer má číslo konvertované)
  57 + 44 = 101.
  V dalším kroku odečteme od posledních dvou cifer součtu číslo 4
  0 - 4 = -4     a     1 - 4 = -3.
  Výsledek: 143.
• Chceme-li zapsat 143 v klasické desítkové soustavě, spočteme rozdíl kladné a záporné části:
  100 - 43 = 57.
  Výsledek: 57.

Program na Cauchyovo komplementární násobení.

Násobení v binární soustavě a redundantní binární soustavě není pro člověka běžné. Lidé totiž díky deseti prstům provádějí výpočty v soustavě desítkové, tj. čísla zapisují pomocí mocnin desítky a cifer od 0 do 9. Se soustavou binární ovšem pracuje valná většina počítačů.

1. Binární soustava
   Každé přirozené číslo n lze právě jedním způsobem vyjádřit ve tvaru:
   n = a_k2^k + a_k-12^k-1 + ... + a₁2¹ + a₀2⁰,
   kde koeficienty a_k, a_k-1, ..., a₁, a₀ nabývají hodnot nula nebo jedna. Řetězci a_k a_k-1 ... a₁ a₀ říkáme binární zápis čísla n. Připomeňme, že binární zápis se získá hladovým algoritmem:
   • Chceme-li najít binární zápis čísla 13, podíváme se, jakou nejvyšší mocninu dvojky číslo 13 obsahuje. To je 8. Poté od 13 odečteme 8 a pro získaný rozdíl 5 opět najdeme největší mocninu dvojky, kterou číslo 5 obsahuje. To je 4. Na závěr spočteme rozdíl 5 - 4 = 1, a to je nultá mocnina dvojky.
   • Získáme 13 = 8 + 4 + 1, a tedy číslo 13 má v binární soustavě zápis 1101.
   Násobení v binární soustavě je velmi podobné jako nám známé klasické násobení v desítkové soustavě. Například číslo 11 s binárním zápisem 1011 a číslo 5 s binárním zápisem 101 se vynásobí následujícím způsobem:
   
   Výsledek je 32 + 16 + 4 + 2 + 1 = 55. Všimněme si, že rychlost násobení odpovídá počtu jedniček v binárním zápisu násobitele (v našem případě jsou dvě jedničky v binárním zápisu 5), právě tolik sčítání totiž musíme provést.
   Program na binární násobení.
2. Redundantní binární soustava
   Připusťme nyní v binární soustavě cifry -1, 0 a 1. Zápisy čísel už nejsou jediné možné, soustava je redundantní. Například 15 = 8 + 4 + 2 + 1 a taky 15 = 16 - 1, tedy jak 1111 tak i 10001 jsou zápisy 15 v redundantní binární soustavě. Vyberme zápis s maximálním počtem nul. K tomu stačí aplikovat následující přepisovací pravidla, dokud je co přepisovat:

   01111 → 10001

   01111 → 10001

   11 → 01

   11 → 01

   Zatímco průměrný počet nul ve standardním binárním zápisu je 1/2, v redundantním binárním zápisu s maximálním možným počtem nul jsou to 2/3. Jelikož je rychlost násobení úměrná počtu nul, je jasné, že redundantní binární soustava je pro násobení velkých čísel výhodnější. Na závěr ještě poznamenejme, že násobíme analogicky jako v klasické binární soustavě. Pouze u znamének dáváme pozor: při násobení cifer stejného znaménka má výsledek znaménko plus, při násobení cifer opačného znaménka má výsledek znaménko mínus. Tedy například násobení 11 a 5 proběhne následovně:
   
   Výsledek je tedy 64 - 8 - 1 = 55.

Program na násobení v redundantní binární soustavě.