Další: 6. Metody vyšetřování Výš: Obsah Předchozí: 4. Geometrické vlastnosti

5. Teorie Howlanda a Yajimy

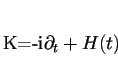
Ke konci 80. let položili J.S. Howland a K. Yajima [3,4] základy matematické teorie časově závislých kvantových systémů a otevřeli tak cestu k jejich systematickému zkoumání. Základním pojmem je Floquetův hamiltonián (nazývaný též operátor kvazienergie)

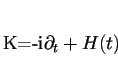
$\begin{displaymath} % latex2html id marker 1418K=-\mathrm{i}\partial _{t}+H(t)\end{displaymath}$

(čili úplný Schródingerův operátor včetně derivace podle $t$ ), který působí v případě periodické časové závislosti v Hilbertově prostoru

$\begin{displaymath} % latex2html id marker 1419\mathcal{K}=L^{2}([\, 0,T\, ],\... ...\mathcal{H}\cong L^{2}([\, 0,T\, ],\mathcal{H},\mathrm{d}t)\, ,\end{displaymath}$

přičemž časová derivace $% latex2html id marker 1042 $ -\mathrm{i}\partial _{t} $$ se bere s periodickou okrajovou podmínkou.

Věta (Howland, Yajima 1979)

V případě periodických časově závislých systémů s periodou $T$ operátory $% latex2html id marker 1044 $ e^{-\mathrm{i}TK} $$ a $% latex2html id marker 1045 $ \mathbb{I}\otimes U(T,0) $$ jsou unitárně ekvivalentní.

Důsledkem této větu je, že charakter spektra operátoru monodromie $U(T,0)$ je stejný jako charakter spektra Floquetova hamiltoniánu $K$ .

Pavel Stovicek
2003-03-26