Krok za krokem k řešení soustav lineárních algebraických rovnic

Obsah

• Kapitola první - Historie
• Úvod
• Soustava lineárních rovnic
• Dávná historie
• Determinant
• Seznam programů

Úvod: Historie lineární algebry je otočená "nohama vzhůru". Odvíjela se totiž v opačném pořadí, než jak se dnes běžně vyučuje v prvním ročníku vysokých škol technického směru. Paradoxně se tedy nejprve objevily determinanty, až po nich matice a teprve začátkem 20. století se začal prosazovat pojem vektorový prostor. Úplně na začátku všeho stály a celým vývojem prostupovaly soustavy lineárních algebraických rovnic. Vždyť také algebra má původ ve slově al-jabr, které použil jako první v 9. století arabský matematik Al-Khwarizmi pro označení "sečtení 2 rovnic s cílem zbavit se neznámé".
Termín soustava lineárních algebraických rovnic: Prozraďme nyní, co je to soustava LAR. Nechť je dáno m.n koeficientů a_ij a m koeficientů pravé strany b_i. My budeme uvažovat ve valné většině úloh koeficienty reálné, ale samozřejmě v historii vždy počtáři pracovali s takovými čísly, která znali. Nejprve s přirozenými, poté racionálními kladnými a zápornými celými čísly, nakonec s reálnými a komplexními a dnes umíme pracovat i s koeficienty ještě obecnějšími, což ale v tuto chvíli není předmětem našeho zájmu. Řešit soustavu m lineárních algebraických rovnic o n neznámých znamená najít reálnou n-tici čísel (x₁, x₂, ..., x_n), která splňují následující rovnice. Termín lineární souvisí s tím, že se neznámé x_i vyskytují v první mocnině, tedy pouze jako (x_i)¹.
Velmi užitečné jsou pojmy matice soustavy a rozšířená matice soustavy. Získáme je tak, že koeficienty sestavíme do tabulek následujícím způsobem. Ukažme si konkrétní příklad takové soustavy a najděme rovnou i její řešení.

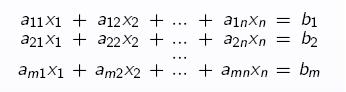
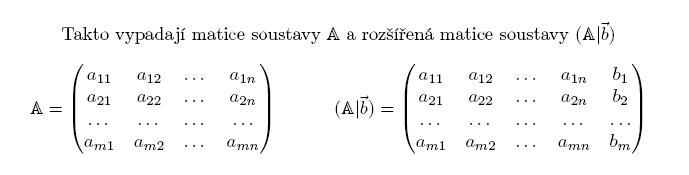
Zde je k dispozici program, který metodami analogickými předchozímu příkladu hledá řešení jakékoliv soustavy 3 rovnic pro 3 neznámé, ovšem za podmínky, že tato soustava má řešení jediné.

Všimněme si, že v předchozím příkladu jsme byli schopni soustavu vyřešit, protože umíme pracovat se zápornými čísly a se zlomky. Počtáři a matematici v dřívějších dobách však ještě naši znalosti neměli a teprve je budovali. Podívejme se, jaké koeficienty a jaké výsledky v rovnicích připouštěli a také jak postupně tvořili matematické značení.

Dávná historie: Egypťané a Babyloňané již před 4000 lety řeší soustavy 2 LAR o 2 neznámých. Takové úlohy zapisují pouze slovně, vždy řeší soustavy s konkrétními číselnými koeficienty, které mají původ v praktických úlohách (Egypťané počítají měřice ječmene a Babylonci gury obilí). Koeficienty jsou jen přirozená čísla a jako výsledek připouští i jednoduché zlomky.

150 - 50 př. n. l. Číňané v 8. kapitole Devíti traktátů o matematickém umění (také se někdy říká Matematika v devíti kapitolách) řeší 18 slovních úloh vedoucích na soustavy LAR, používají metodu fang čcheng, která je předchůdkyní Gaussova eliminačního algoritmu a používá sloupcové úpravy. Čínští počtáři umí pracovat s přirozenými čísly a jednoduchými zlomky, ale v mezivýpočtech připouští i čísla záporná, definují základní aritmetické operace s takovými čísly, ale barví je červenou tuší a nepovažují je ještě za plnohodnotná čísla.

Japonec Takakazu Šinsuke Seki Kowa (1642-1708) a jeho žáci rozvíjí metodu fang čcheng a jejím prostřednictvím dospívají k pojmu determinant. Seki Kowa (na obrázku) bývá občas považován za objevitele determinantu.

Staří Řekové, ač jsou považováni za zakladatele opravdové matematiky (Eukleides stojí u zrodu toho nejdůležitějšího v celé matematice - nutnosti tvrzení dokázat), k rozvoji řešení soustav LAR významně nepřispěli. Jedním z důvodů je jejich složitá číselná soustava, v níž se aritmetické výpočty prováděli obtížně, druhým pak jejich zájem zaostřený na geometrii. Právě kvůli geometrii pracují jen s kladnými racionálními čísly (záporná čísla nemohou představovat délku úsečky či obsah nějakého útvaru).

Teprve indický učenec Brahmagupta přichází v 7. stol. s definicí nuly jakožto čísla (poziční nula, která značí prázdné místo v zápisu čísel v pozičních číselných soustavách, má kořeny již ve staré Babylonii). Brahmagupta definuje operace s nulou a se zápornými čísly (představuje si je jako dluh). Od této chvíle se koeficienty i výsledky v soustavách LAR mohou pohybovat i v oblasti záporných čísel. Další indickou zajímavostí je, že neznámým dávají jména barev. Do středověké Evropy se indické poznatky dostávají prostřednictvím Arabů.

Do 17. století: V 16. stol. se začíná vytvářet algebraická symbolika. François Viète v Analytickém umění značí neznámé samohláskami a koeficienty souhláskami a užívá dnešní znaky pro plus a mínus +,-. Navíc jako první vyjadřuje tvar řešení soustavy v závislosti na koeficientech - i slovo koeficient je od něj. Dnešní značení se poprvé objevuje u Reného Descarta: koeficienty značí a, b, c, ...neznámé x, y, z,... a soustavu zapisuje tak, že je na pravé straně každé rovnice nula.

Determinant: Ukažme si nejprve, jak spočíst determinant matice rozměru 2 x 2 a 3 x 3 (matici si představujme jako tabulku čísel). Obecnou definici determinantu najdete ve skriptech Algebra 2 .

Za objevitele determinantu bývá obvykle považován Gottfried Wilhelm Leibniz (1646 Lipsko - 1716 Hannover). V roce 1693 píše dopis markýzi L’Hospitalovi, ve kterém tvrdí, že pokud soustava n + 1 LAR o n neznámých s pravou stranou má řešení, pak je nutně determinant rozšířené matice soustavy nulový. Nepoužívá ještě ovšem slovo determinant, protože takové označení použije poprvé až Gauss, a samozřejmě ani matice, poněvadž s tím přijde ještě o něco později Sylvester. Leibniz v dopise chválí své novátorské značení: ij pro koeficient a_ij a j0 pro j -tou složku pravé strany b_j. Popis vytváření determinantu je nepraktický, a tak jeho nápad zůstává bez ohlasu.