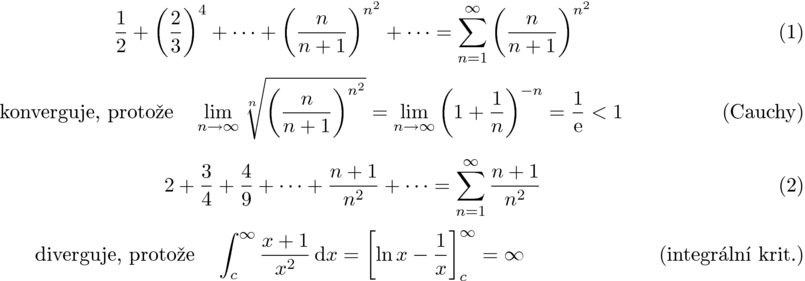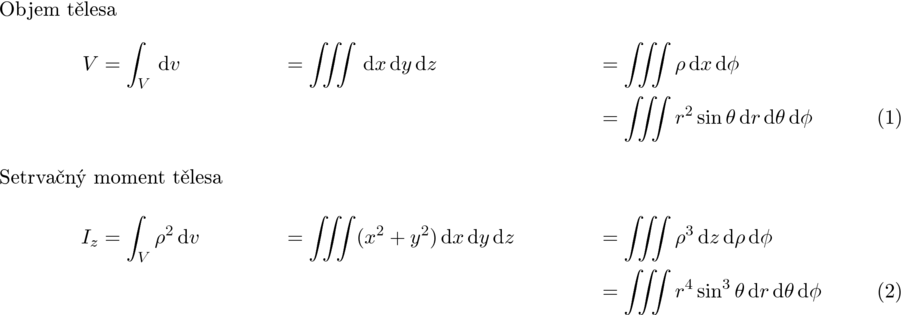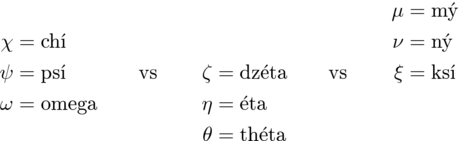01PSL

1

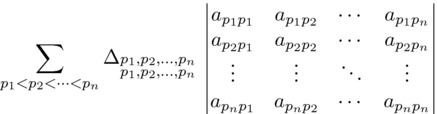
nebo

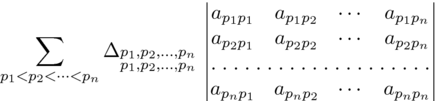
Matematika:

    p_1, p_2, p_n
    
    a_{p_1p_1} & a_{p_1p_2} & a_{p_1p_n} \\
    a_{p_2p_1} & a_{p_2p_2} & a_{p_2p_n} \\
    a_{p_np_1} & a_{p_np_2} & a_{p_np_n}

→ Zobraz nápovědu

\substack{ ... \\ ...}

víceřádkový index

Výpustky v matematice

\ldots	horizontální tečky na účaří
\cdots	horizontální tečky, vertikálně na úrovni bin. operátorů
\vdots	vertikální tečky
\ddots	diagonální tečky
\hdotsfor[roztec]{n}	pokračovací řádek přes n sloupců
	parametr roztec určuje vzájemnou vzdálenost sousedních teček

→ Zobraz řešení

      \sum_{p_1<p_2<\cdots<p_n}
      \Delta_{\substack{p_1,p_2,\ldots,p_n\\p_1,p_2,\ldots,p_n}}
      \begin{vmatrix}
        a_{p_1p_1} & a_{p_1p_2} & \cdots & a_{p_1p_n} \\
        a_{p_2p_1} & a_{p_2p_2} & \cdots & a_{p_2p_n} \\
        \vdots     & \vdots     & \ddots & \vdots \\
        a_{p_np_1} & a_{p_np_2} & \cdots & a_{p_np_n}
      \end{vmatrix}

2

(celé cvičení jako jedno prostředí gather)

Matematika:

  \frac{1}{2} + \left(\frac{2}{3}\right)^4 + \cdots + \left(\frac{n}{n+1}\right)^{n^2}
  + \cdots = \sum_{n=1}^\infty \left(\frac{n}{n+1}\right)^{n^2}
  \lim_{n\rightarrow\infty}\sqrt[n]{\left(\frac{n}{n+1}\right)^{n^2}} =
  \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^{-n} = \frac{1}{\mathrm{e}} < 1
  2 + \frac{3}{4} + \frac{4}{9} + \cdots + \frac{n+1}{n^2} + \cdots =
  \sum_{n=1}^\infty \frac{n+1}{n^2} \int_c^\infty\frac{x+1}{x^2}\,\mathrm{d}x = 
  \left[\ln x-\frac{1}{x}\right]_c^\infty = \infty

→ Zobraz nápovědu

Víceřádkové rovnice

\\[delka]	přechod na nový řádek
\tag{znacka}	změna čísla/značky rovnice
\notag	potlačení sazby čísla rovnice

→ Zobraz řešení

      \begin{gather}
      
      \end{gather}

3

(celé cvičení jako jedno prostředí align)

Matematika:

→ Zobraz nápovědu

\intertext	příkaz pro vložení krátkého textu mezi dva řádky zarovnaných rovnic
	místo zarovnání zůstane zachováno

4

(pro sazbu použijte tři prostředí aligned)

→ Zobraz nápovědu

Obě prostředí pro sazbu zarovnaných "stavebních bloků", tj. aligned a gathered mají volitelný parametr pozice, možné hodnoty: t a b, který určuje vertikální zarovnání nacházejí-li se prostředí mezi dalšími elementy.

5

→ Zobraz nápovědu

Velikost matematického fontu určuje LaTeX automaticky. V situacích, kdy automatické nastavení nevyhovuje je možné velikost fontu předepsat ručně pomocí příkazů

\displaystyle	výchozí velikost písma v mat. módu "na displayi"
\textstyle	výchozí velikost písma v mat. módu "v rámci odstavce"
\scriptstyle	výchozí velikost písma indexů
\scriptscriptstyle	výchozí velikost písma indexů indexů

Pro snadnější vysázení řetězového zlomku je možné použít příkaz (z AMSLaTeXu)

\cfrac{}{}

4. cvičení — balíček AMSLaTeX